Curve

class rateslib.curves.Curve(nodes, *, interpolation=NoInput.blank, t=NoInput.blank, c=NoInput.blank, endpoints=NoInput.blank, id=NoInput.blank, convention=NoInput.blank, modifier=NoInput.blank, calendar=NoInput.blank, ad=0, index_base=NoInput.blank, index_lag=NoInput.blank, **kwargs)

Bases: _WithState, _WithCache[datetime, Dual | Dual2 | Variable | float]

Curve based on DF parametrisation at given node dates with interpolation.

Parameters:

• nodes (dict[datetime: float]) – Parameters of the curve denoted by a node date and a corresponding DF at that point.

• interpolation (str or callable) – The interpolation used in the non-spline section of the curve. That is the part of the curve between the first node in nodes and the first knot in t. If a callable, this allows a user-defined interpolation scheme, and this must have the signature method(date, nodes), where date is the datetime whose DF will be returned and nodes is as above and is passed to the callable.

• t (list[datetime], optional) – The knot locations for the B-spline log-cubic interpolation section of the curve. If None all interpolation will be done by the local method specified in interpolation.

• c (list[float], optional) – The B-spline coefficients used to define the log-cubic spline. If not given, which is the expected case, uses csolve() to calculate these automatically.

• endpoints (2-tuple of str, optional) – The left and then right endpoint constraint for the spline solution. Valid values are in {“natural”, “not_a_knot”}.

• id (str, optional, set by Default) – The unique identifier to distinguish between curves in a multicurve framework.

• convention (str, optional, set by Default) – The convention of the curve for determining rates. Please see dcf() for all available options.

• modifier (str, optional) – The modification rule, in {“F”, “MF”, “P”, “MP”}, for determining rates.

• calendar (calendar or str, optional) – The holiday calendar object to use. If str, looks up named calendar from static data. Used for determining rates.

• ad (int in {0, 1, 2}, optional) – Sets the automatic differentiation order. Defines whether to convert node values to float, Dual or Dual2. It is advised against using this setting directly. It is mainly used internally.

• index_base (float, optional) – The initial index value at the initial node date of the curve. Used for forecasting future index values.

• index_lag (int, optional) – Number of months of by which the index lags the date. For example if the initial curve node date is 1st Sep 2021 based on the inflation index published 17th June 2023 then the lag is 3 months.

Notes

This curve type is discount factor (DF) based and is parametrised by a set of (date, DF) pairs set as nodes. The initial node date of the curve is defined to be today and should always have a DF of precisely 1.0. The initial DF will not be affected by a Solver.

Intermediate DFs are determined through interpolation. If local interpolation is adopted a DF for an arbitrary date is dependent only on its immediately neighbouring nodes via the interpolation routine. Available options are:

• “log_linear” (default for this curve type)

• “linear_index”

And also the following which are not recommended for this curve type:

• “linear”,

• “linear_zero_rate”,

• “flat_forward”,

• “flat_backward”,

Global interpolation in the form of a log-cubic spline is also configurable with the parameters t, c and endpoints. See splines for instruction of knot sequence calibration. Values before the first knot in t will be determined through the local interpolation method.

For defining rates by a given tenor, the modifier and calendar arguments will be used. For correct scaling of the rate a convention is attached to the curve, which is usually one of “Act360” or “Act365F”.

Examples

In [1]: curve = Curve(
   ...:     nodes={
   ...:         dt(2022,1,1): 1.0,  # <- initial DF should always be 1.0
   ...:         dt(2023,1,1): 0.99,
   ...:         dt(2024,1,1): 0.979,
   ...:         dt(2025,1,1): 0.967,
   ...:         dt(2026,1,1): 0.956,
   ...:         dt(2027,1,1): 0.946,
   ...:     },
   ...:     interpolation="log_linear",
   ...: )
   ...: 

In [2]: curve.plot("1d")
Out[2]: 
(<Figure size 640x480 with 1 Axes>,
 <Axes: >,
 [<matplotlib.lines.Line2D at 0x112afad50>])

(Source code, png, hires.png, pdf)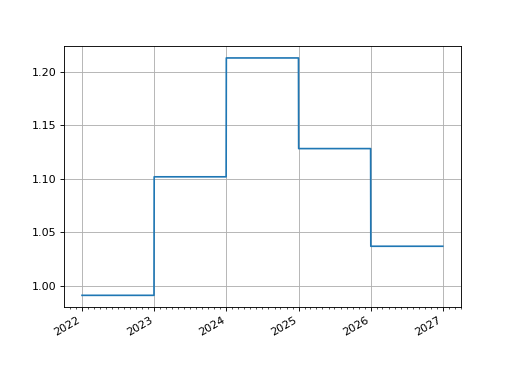

Attributes Summary

ad
collateral

Methods Summary

copy()	Create an identical copy of the curve object.
csolve()	Solves and sets the coefficients, c, of the PPSpline.
from_json(curve, **kwargs)	Reconstitute a curve from JSON.
index_value(date[, interpolation])	Calculate the accrued value of the index from the index_base.
plot(tenor[, right, left, comparators, ...])	Plot given forward tenor rates from the curve.
plot_index([right, left, comparators, ...])	Plot given forward tenor rates from the curve.
rate(effective, termination[, modifier, ...])	Calculate the rate on the Curve using DFs.
roll(tenor)	Create a new curve with its shape translated in time but an identical initial node date.
shift(spread[, id, composite, collateral])	Create a new curve by vertically adjusting the curve by a set number of basis points.
to_json()	Convert the parameters of the curve to JSON format.
translate(start[, t])	Create a new curve with an initial node date moved forward keeping all else constant.
update([nodes, interpolation, endpoints])	Update a curve with new, manually input values.
update_node(key, value)	Update a single node value on the Curve.

Attributes Documentation

ad

collateral = None

Methods Documentation

copy()

Create an identical copy of the curve object.

Return type:

Curve or LineCurve

csolve()

Solves and sets the coefficients, c, of the PPSpline.

Return type:

None

Notes

Only impacts curves which have a knot sequence, t, and a PPSpline. Only solves if c not given at curve initialisation.

Uses the spline_endpoints attribute on the class to determine the solving method.

classmethod from_json(curve, **kwargs)

Reconstitute a curve from JSON.

Parameters:

curve (str) – The JSON string representation of the curve.

Return type:

Curve or LineCurve

index_value(date, interpolation='daily')

Calculate the accrued value of the index from the index_base.

Parameters:

• date (datetime) – The date for which the index value will be returned.

• interpolation (str in {"monthly", "daily"}) – The method for returning the index value. Monthly returns the index value for the start of the month and daily returns a value based on the interpolation between nodes (which is recommended “linear_index) for InflationCurve.

Return type:

None, float, Dual, Dual2

Examples

The SWESTR rate, for reference value date 6th Sep 2021, was published as 2.375% and the RFR index for that date was 100.73350964. Below we calculate the value that was published for the RFR index on 7th Sep 2021 by the Riksbank.

In [1]: index_curve = Curve(
   ...:     nodes={
   ...:         dt(2021, 9, 6): 1.0,
   ...:         dt(2021, 9, 7): 1 / (1 + 2.375/36000)
   ...:     },
   ...:     index_base=100.73350964,
   ...:     convention="Act360",
   ...: )
   ...: 

In [2]: index_curve.rate(dt(2021, 9, 6), "1d")
Out[2]: 2.3750000000015703

In [3]: index_curve.index_value(dt(2021, 9, 7))
Out[3]: 100.7401552534832

plot(tenor, right=NoInput.blank, left=NoInput.blank, comparators=NoInput.blank, difference=False, labels=NoInput.blank)

Plot given forward tenor rates from the curve. See notes.

Parameters:

• tenor (str) – The tenor of the forward rates to plot, e.g. “1D”, “3M”.

• right (datetime or str, optional) – The right bound of the graph. If given as str should be a tenor format defining a point measured from the initial node date of the curve. Defaults to the final node of the curve minus the tenor.

• left (datetime or str, optional) – The left bound of the graph. If given as str should be a tenor format defining a point measured from the initial node date of the curve. Defaults to the initial node of the curve.

• comparators (list[Curve]) – A list of curves which to include on the same plot as comparators.

• difference (bool) – Whether to plot as comparator minus base curve or outright curve levels in plot. Default is False.

• labels (list[str]) – A list of strings associated with the plot and comparators. Must be same length as number of plots.

Returns:

(fig, ax, line)

Return type:

Matplotlib.Figure, Matplotplib.Axes, Matplotlib.Lines2D

Notes

This function plots single-period, simple interest curve rates, which are defined as:

\[1 + r d = \frac{v_{start}}{v_{end}}\]

where d is the day count fraction determined using the convention associated with the Curve.

This function does not plot swap rates, which is impossible since the Curve object contains no information regarding the parameters of the ‘swap’ (e.g. its frequency or its convention etc.). If tenors longer than one year are sought results may start to deviate from those one might expect. See Issue 246.

plot_index(right=NoInput.blank, left=NoInput.blank, comparators=NoInput.blank, difference=False, labels=NoInput.blank)

Plot given forward tenor rates from the curve.

Parameters:

• tenor (str) – The tenor of the forward rates to plot, e.g. “1D”, “3M”.

• right (datetime or str, optional) – The right bound of the graph. If given as str should be a tenor format defining a point measured from the initial node date of the curve. Defaults to the final node of the curve minus the tenor.

• left (datetime or str, optional) – The left bound of the graph. If given as str should be a tenor format defining a point measured from the initial node date of the curve. Defaults to the initial node of the curve.

• comparators (list[Curve]) – A list of curves which to include on the same plot as comparators.

• difference (bool) – Whether to plot as comparator minus base curve or outright curve levels in plot. Default is False.

• labels (list[str]) – A list of strings associated with the plot and comparators. Must be same length as number of plots.

Returns:

(fig, ax, line)

Return type:

Matplotlib.Figure, Matplotplib.Axes, Matplotlib.Lines2D

rate(effective, termination, modifier=NoInput.inherit, float_spread=NoInput.blank, spread_compound_method=NoInput.blank)

Calculate the rate on the Curve using DFs.

If rates are sought for dates prior to the initial node of the curve None will be returned.

Parameters:

• effective (datetime) – The start date of the period for which to calculate the rate.

• termination (datetime or str) – The end date of the period for which to calculate the rate.

• modifier (str, optional) – The day rule if determining the termination from tenor. If False is determined from the Curve modifier.

• float_spread (float, optional) – A float spread can be added to the rate in certain cases.

• spread_compound_method (str in {"none_simple", "isda_compounding"}) – The method if adding a float spread. If “none_simple” is used this results in an exact calculation. If “isda_compounding” or “isda_flat_compounding” is used this results in an approximation.

Return type:

Dual, Dual2 or float

Notes

Calculating rates from a curve implies that the conventions attached to the specific index, e.g. USD SOFR, or GBP SONIA, are applicable and these should be set at initialisation of the Curve. Thus, the convention used to calculate the rate is taken from the Curve from which rate is called.

modifier is only used if a tenor is given as the termination.

Major indexes, such as legacy IBORs, and modern RFRs typically use a convention which is either “Act365F” or “Act360”. These conventions do not need additional parameters, such as the termination of a leg, the frequency or a leg or whether it is a stub to calculate a DCF.

Adding Floating Spreads

An optimised method for adding floating spreads to a curve rate is provided. This is quite restrictive and mainly used internally to facilitate other parts of the library.

• When spread_compound_method is “none_simple” the spread is a simple linear addition.

• When using “isda_compounding” or “isda_flat_compounding” the curve is assumed to be comprised of RFR rates and an approximation is used to derive to total rate.

Examples

In [1]: curve_act365f = Curve(
   ...:     nodes={
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2022, 2, 1): 0.98,
   ...:         dt(2022, 3, 1): 0.978,
   ...:     },
   ...:     convention='Act365F'
   ...: )
   ...: 

In [2]: curve_act365f.rate(dt(2022, 2, 1), dt(2022, 3, 1))
Out[2]: 2.6657902424774402

Using a different convention will result in a different rate:

In [3]: curve_act360 = Curve(
   ...:     nodes={
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2022, 2, 1): 0.98,
   ...:         dt(2022, 3, 1): 0.978,
   ...:     },
   ...:     convention='Act360'
   ...: )
   ...: 

In [4]: curve_act360.rate(dt(2022, 2, 1), dt(2022, 3, 1))
Out[4]: 2.6292725679229547

roll(tenor)

Create a new curve with its shape translated in time but an identical initial node date.

This curve adjustment is a simulation of a future state of the market where forward rates are assumed to have moved so that the present day’s curve shape is reflected in the future (or the past). This is often used in trade strategy analysis.

Parameters:

tenor (datetime or str) – The date or tenor by which to roll the curve. If a tenor, as str, will derive the datetime as measured from the initial node date. If supplying a negative tenor, or a past datetime, there is a limit to how far back the curve can be rolled - it will first roll backwards and then attempt to translate() forward to maintain the initial node date.

Return type:

Curve

Examples

The basic use of this function translates a curve forward in time and the plot demonstrates its rates are exactly the same as initially forecast.

In [1]: curve = Curve(
   ...:     nodes = {
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2023, 1, 1): 0.988,
   ...:         dt(2024, 1, 1): 0.975,
   ...:         dt(2025, 1, 1): 0.965,
   ...:         dt(2026, 1, 1): 0.955,
   ...:         dt(2027, 1, 1): 0.9475
   ...:     },
   ...:     t = [
   ...:         dt(2024, 1, 1), dt(2024, 1, 1), dt(2024, 1, 1), dt(2024, 1, 1),
   ...:         dt(2025, 1, 1),
   ...:         dt(2026, 1, 1),
   ...:         dt(2027, 1, 1), dt(2027, 1, 1), dt(2027, 1, 1), dt(2027, 1, 1),
   ...:     ],
   ...: )
   ...: 

In [2]: rolled_curve = curve.roll("6m")

In [3]: rolled_curve2 = curve.roll("-6m")

In [4]: curve.plot(
   ...:     "1d",
   ...:     comparators=[rolled_curve, rolled_curve2],
   ...:     labels=["orig", "rolled", "rolled2"],
   ...:     right=dt(2026, 6, 30),
   ...: )
   ...: 
Out[4]: 
(<Figure size 640x480 with 1 Axes>,
 <Axes: >,
 [<matplotlib.lines.Line2D at 0x112fe6c10>,
  <matplotlib.lines.Line2D at 0x112fe6d50>,
  <matplotlib.lines.Line2D at 0x112fe6e90>])

(Source code, png, hires.png, pdf)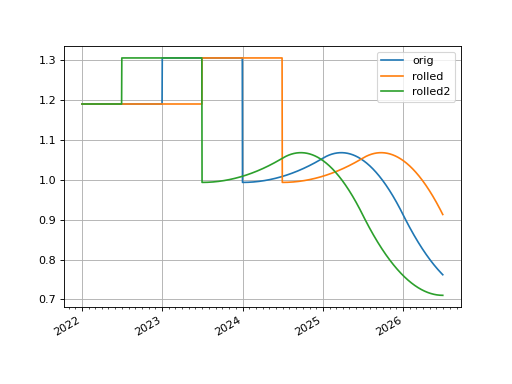

shift(spread, id=NoInput.blank, composite=True, collateral=NoInput.blank)

Create a new curve by vertically adjusting the curve by a set number of basis points.

This curve adjustment preserves the shape of the curve but moves it up or down as a translation. This method is suitable as a way to assess value changes of instruments when a parallel move higher or lower in yields is predicted.

Parameters:

• spread (float, Dual, Dual2) –

  The number of basis points added to the existing curve.

  Warning

  If composite is True, users must be aware that adding Dual or Dual2 spreads must be compatible with the AD order of Self, otherwise TypeErrors may be raised. If in doubt, only use float spread values.

• id (str, optional) – Set the id of the returned curve.

• composite (bool, optional) – If True will return a CompositeCurve that adds a flat curve to the existing curve. This results in slower calculations but the curve will maintain a dynamic association with the underlying curve and will change if the underlying curve changes.

• collateral (str, optional) – Designate a collateral tag for the curve which is used by other methods.

Return type:

Curve, CompositeCurve

Examples

In [1]: from rateslib.curves import Curve

In [2]: curve = Curve(
   ...:     nodes = {
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2023, 1, 1): 0.988,
   ...:         dt(2024, 1, 1): 0.975,
   ...:         dt(2025, 1, 1): 0.965,
   ...:         dt(2026, 1, 1): 0.955,
   ...:         dt(2027, 1, 1): 0.9475
   ...:     },
   ...:     t = [
   ...:         dt(2024, 1, 1), dt(2024, 1, 1), dt(2024, 1, 1), dt(2024, 1, 1),
   ...:         dt(2025, 1, 1),
   ...:         dt(2026, 1, 1),
   ...:         dt(2027, 1, 1), dt(2027, 1, 1), dt(2027, 1, 1), dt(2027, 1, 1),
   ...:     ],
   ...: )
   ...: 

In [3]: shifted_curve = curve.shift(25)

In [4]: curve.plot("1d", comparators=[shifted_curve], labels=["orig", "shift"])
Out[4]: 
(<Figure size 640x480 with 1 Axes>,
 <Axes: >,
 [<matplotlib.lines.Line2D at 0x1132c3c50>,
  <matplotlib.lines.Line2D at 0x1132c3d90>])

(Source code, png, hires.png, pdf)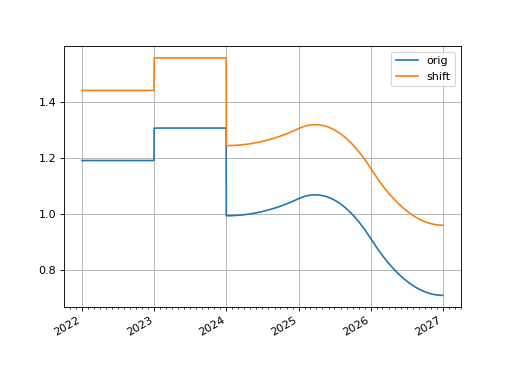

to_json()

Convert the parameters of the curve to JSON format.

Return type:

str

translate(start, t=False)

Create a new curve with an initial node date moved forward keeping all else constant.

This curve adjustment preserves forward curve expectations as time evolves. This method is suitable as a way to create a subsequent opening curve from a previous day’s closing curve.

Parameters:

• start (datetime) – The new initial node date for the curve, must be in the domain: (node_date[0], node_date[1]]

• t (bool) – Set to True if the initial knots of the knot sequence should be translated forward.

Return type:

Curve

Examples

The basic use of this function translates a curve forward in time and the plot demonstrates its rates are exactly the same as initially forecast.

In [1]: curve = Curve(
   ...:     nodes = {
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2023, 1, 1): 0.988,
   ...:         dt(2024, 1, 1): 0.975,
   ...:         dt(2025, 1, 1): 0.965,
   ...:         dt(2026, 1, 1): 0.955,
   ...:         dt(2027, 1, 1): 0.9475
   ...:     },
   ...:     t = [
   ...:         dt(2024, 1, 1), dt(2024, 1, 1), dt(2024, 1, 1), dt(2024, 1, 1),
   ...:         dt(2025, 1, 1),
   ...:         dt(2026, 1, 1),
   ...:         dt(2027, 1, 1), dt(2027, 1, 1), dt(2027, 1, 1), dt(2027, 1, 1),
   ...:     ],
   ...: )
   ...: 

In [2]: translated_curve = curve.translate(dt(2022, 12, 1))

In [3]: curve.plot(
   ...:     "1d",
   ...:     comparators=[translated_curve],
   ...:     labels=["orig", "translated"],
   ...:     left=dt(2022, 12, 1),
   ...: )
   ...: 
Out[3]: 
(<Figure size 640x480 with 1 Axes>,
 <Axes: >,
 [<matplotlib.lines.Line2D at 0x113624e10>,
  <matplotlib.lines.Line2D at 0x113624f50>])

(Source code, png, hires.png, pdf)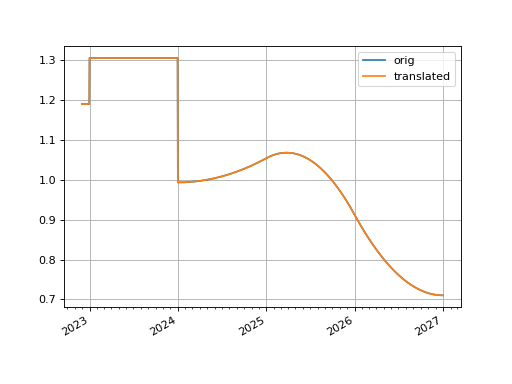

In [4]: curve.nodes
Out[4]: 
{datetime.datetime(2022, 1, 1, 0, 0): 1.0,
 datetime.datetime(2023, 1, 1, 0, 0): 0.988,
 datetime.datetime(2024, 1, 1, 0, 0): 0.975,
 datetime.datetime(2025, 1, 1, 0, 0): 0.965,
 datetime.datetime(2026, 1, 1, 0, 0): 0.955,
 datetime.datetime(2027, 1, 1, 0, 0): 0.9475}

In [5]: translated_curve.nodes
Out[5]: 
{datetime.datetime(2022, 12, 1, 0, 0): 1.0,
 datetime.datetime(2023, 1, 1, 0, 0): 0.9989751829682344,
 datetime.datetime(2024, 1, 1, 0, 0): 0.9858307726660208,
 datetime.datetime(2025, 1, 1, 0, 0): 0.9757196878181642,
 datetime.datetime(2026, 1, 1, 0, 0): 0.9656086029703076,
 datetime.datetime(2027, 1, 1, 0, 0): 0.9580252893344151}

When a curve has a log-cubic spline the knot dates can be preserved or translated with the t argument. Preserving the knot dates preserves the interpolation of the curve. A knot sequence for a mixed curve which begins after start will not be affected in either case.

In [6]: curve = Curve(
   ...:     nodes={
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2022, 2, 1): 0.999,
   ...:         dt(2022, 3, 1): 0.9978,
   ...:         dt(2022, 4, 1): 0.9963,
   ...:         dt(2022, 5, 1): 0.9940
   ...:     },
   ...:     t = [dt(2022, 1, 1), dt(2022, 1, 1), dt(2022, 1, 1), dt(2022, 1, 1),
   ...:          dt(2022, 2, 1), dt(2022, 3, 1), dt(2022, 4, 1),
   ...:          dt(2022, 5, 1), dt(2022, 5, 1), dt(2022, 5, 1), dt(2022, 5, 1)]
   ...: )
   ...: 

In [7]: translated_curve = curve.translate(dt(2022, 1, 15))

In [8]: translated_curve2 = curve.translate(dt(2022, 1, 15), t=True)

In [9]: curve.plot("1d", left=dt(2022, 1, 15), comparators=[translated_curve, translated_curve2], labels=["orig", "translated", "translated2"])
Out[9]: 
(<Figure size 640x480 with 1 Axes>,
 <Axes: >,
 [<matplotlib.lines.Line2D at 0x1138c42d0>,
  <matplotlib.lines.Line2D at 0x1138c4410>,
  <matplotlib.lines.Line2D at 0x1138c4550>])

(Source code, png, hires.png, pdf)

update(nodes=NoInput.blank, interpolation=NoInput.blank, endpoints=NoInput.blank)

Update a curve with new, manually input values.

For arguments see Curve. Any value not given will not change the underlying Curve.

Parameters:

• nodes (dict[datetime, DualTypes], optional) – New nodes to assign to the curve.

• interpolation (str or Callable, optional) – Interpolation method to use.

• endpoints (str or tuple[str, str], optional) – Endpoint constraints to apply to spline interpolation.

Return type:

None

Notes

Warning

Rateslib is an object-oriented library that uses complex associations. Although Python may not object to directly mutating attributes of a Curve instance, this should be avoided in rateslib. Only use official update methods to mutate the values of an existing Curve instance. This class is labelled as a mutable on update object.

update_node(key, value)

Update a single node value on the Curve.

Parameters:

• key (datetime) – The node date to update. Must exist in nodes.

• value (float, Dual, Dual2, Variable) – Value to update on the Curve.

Return type:

None

Notes

Warning

Rateslib is an object-oriented library that uses complex associations. Although Python may not object to directly mutating attributes of a Curve instance, this should be avoided in rateslib. Only use official update methods to mutate the values of an existing Curve instance. This class is labelled as a mutable on update object.