LineCurve#

class rateslib.curves.LineCurve(*args, **kwargs)#

Bases: _WithMutability, _BaseCurve

A _BaseCurve with value parametrisation at given node dates with interpolation.

Parameters:

  • nodes (dict[datetime: float]) – Parameters of the curve denoted by a node date and a corresponding value at that point.

  • interpolation (str in {"log_linear", "linear"} or callable) – The interpolation used in the non-spline section of the curve. That is the part of the curve between the first node in nodes and the first knot in t. If a callable, this allows a user-defined interpolation scheme, and this must have the signature method(date, nodes), where date is the datetime whose DF will be returned and nodes is as above and is passed to the callable.

  • t (list[datetime], optional) – The knot locations for the B-spline cubic interpolation section of the curve. If None all interpolation will be done by the method specified in interpolation.

  • endpoints (str or list, optional) – The left and right endpoint constraint for the spline solution. Valid values are in {“natural”, “not_a_knot”}. If a list, supply the left endpoint then the right endpoint.

  • id (str, optional, set by Default) – The unique identifier to distinguish between curves in a multi-curve framework. convention : str, optional, set by Default The convention of the curve for determining rates. Please see dcf() for all available options.

  • convention (str, optional, set by Default) – The convention of the curve for determining rates. Please see dcf() for all available options.

  • modifier (str, optional) – The modification rule, in {“F”, “MF”, “P”, “MP”}, for determining rates when input as a tenor, e.g. “3M”.

  • calendar (calendar or str, optional) – The holiday calendar object to use. If str, looks up named calendar from static data. Used for determining rates.

  • ad (int in {0, 1, 2}, optional) – Sets the automatic differentiation order. Defines whether to convert node values to float, Dual or Dual2. It is advised against using this setting directly. It is mainly used internally.

Notes

The arguments index_base, index_lag, and collateral available on Curve are not used by, or relevant for, a LineCurve.

This curve type is value based and it is parametrised by a set of (date, value) pairs set as nodes. The initial node date of the curve is defined to be today, and can take a general value. The initial value will be affected by a Solver.

Note

This curve type can only ever be used for forecasting rates and projecting cashflow calculations. It cannot be used to discount cashflows becuase it is not DF based and there is no mathematical one-to-one conversion available to imply DFs.

Intermediate values are determined through interpolation. If local interpolation is adopted a value for an arbitrary date is dependent only on its immediately neighbouring nodes via the interpolation routine. Available options are:

  • “linear” (default for this curve type)

  • “log_linear” (useful for values that exponential, e.g. stock indexes or GDP)

  • “spline”

  • “flat_forward”, (useful for replicating a DF based log-linear type curve)

  • “flat_backward”,

And also the following which are not recommended for this curve type:

  • “linear_index”

  • “linear_zero_rate”,

Spline Interpolation

Global interpolation in the form of a cubic spline is also configurable with the parameters t, and endpoints. Setting an interpolation of “spline” is syntactic sugar for automatically determining the most obvious knot sequence t to use all specified node dates. See splines for instruction of knot sequence calibration.

If the knot sequence is provided directly then any dates prior to the first knot date in t will be determined through the local interpolation method. This allows for mixed interpolation.

This curve type cannot return arbitrary tenor rates. It will only return a single value which is applicable to that date. It is recommended to review RFR and IBOR Indexing to ensure indexing is done in a way that is consistent with internal instrument configuration.

Examples

In [1]: nodes = {
   ...:     dt(2022,1,1): 0.975,  # <- initial value is general
   ...:     dt(2023,1,1): 1.10,
   ...:     dt(2024,1,1): 1.22,
   ...:     dt(2025,1,1): 1.14,
   ...:     dt(2026,1,1): 1.03,
   ...:     dt(2027,1,1): 1.03,
   ...: }
   ...: 

In [2]: line_curve1 = LineCurve(nodes=nodes, interpolation="linear")

In [3]: line_curve2 = LineCurve(nodes=nodes, interpolation="spline")

In [4]: line_curve1.plot("1d", comparators=[line_curve2], labels=["linear", "cubic spline"])
Out[4]: 
(<Figure size 640x480 with 1 Axes>,
 <Axes: >,
 [<matplotlib.lines.Line2D at 0x117429810>,
  <matplotlib.lines.Line2D at 0x117429950>])

(Source code, png, hires.png, pdf)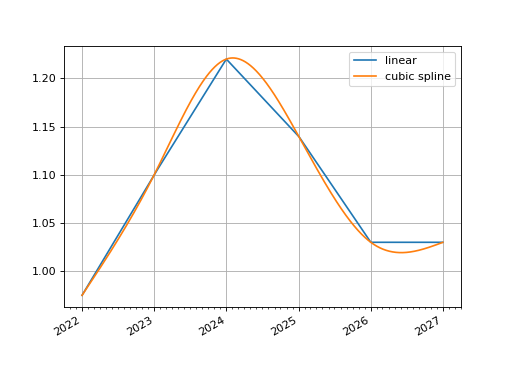

../_images/rateslib-curves-LineCurve-1_00_00.png

Attributes Summary

ad

Int in {0,1,2} describing the AD order associated with the Curve.

id

A str identifier to name the Curve used in Solver mappings.

interpolator

An instance of _CurveInterpolator.

meta

An instance of _CurveMeta.

nodes

An instance of _CurveNodes.

Methods Summary

copy()

Create an identical copy of the curve object.

csolve()

Solves and sets the coefficients, c, of the PPSpline.

index_value(date, index_lag[, interpolation])

Calculate the accrued value of the index from the index_base.

plot(tenor[, right, left, comparators, ...])

Plot given forward tenor rates from the curve.

plot_index([right, left, comparators, ...])

Plot given index values on a Curve.

rate(effective[, termination, modifier, ...])

Calculate the rate on the Curve using DFs.

roll(tenor[, id])

Create a RolledCurve: translating the rate space of Self in time.

shift(spread[, id])

Create a ShiftedCurve: moving Self vertically in rate space.

to_json()

Serialize this object to JSON format.

translate(start[, id])

Create a TranslatedCurve: maintaining an identical rate space, but moving the initial node date forwards in time.

update([nodes])

Update a curves nodes with new, manually input values.

update_meta(key, value)

Update a single meta value on the Curve.

update_node(key, value)

Update a single node value on the Curve.

Attributes Documentation

ad#

Int in {0,1,2} describing the AD order associated with the Curve.

id#

A str identifier to name the Curve used in Solver mappings.

interpolator#

An instance of _CurveInterpolator.

meta#

An instance of _CurveMeta.

nodes#

An instance of _CurveNodes.

Methods Documentation

copy()#

Create an identical copy of the curve object.

Return type:

Self

csolve()#

Solves and sets the coefficients, c, of the PPSpline.

Return type:

None

Notes

Only impacts curves which have a knot sequence, t, and a PPSpline. Only solves if c not given at curve initialisation.

Uses the spline_endpoints attribute on the class to determine the solving method.

index_value(date, index_lag, interpolation='curve')#

Calculate the accrued value of the index from the index_base.

This method will raise if performed on a ‘values’ type Curve.

Parameters:

  • date (datetime) – The date for which the index value will be returned.

  • index_lag (int) – The number of months by which to lag the index when determining the value.

  • interpolation (str in {"curve", "monthly", "daily"}) – The method for returning the index value. Monthly returns the index value for the start of the month and daily returns a value based on the interpolation between nodes (which is recommended “linear_index) for InflationCurve.

Return type:

None, float, Dual, Dual2

Notes

The interpolation methods function as follows:

  • “curve”: will raise if the requested index_lag does not match the lag attributed to the Curve. In the case the index_lag matches, then the index value for any date is derived via the implied interpolation for the discount factors of the Curve.

    \[I_v(m) = \frac{I_b}{v(m)}\]

  • “monthly”: For any date, m, uses the “curve” method having adjusted m in two ways. Firstly it deducts a number of months equal to \(L - L_c\), where L is the given index_lag and \(L_c\) is the index lag of the Curve. And the day of the month is set to 1.

    \[\begin{split}&I^{monthly}_v(m) = I_v(m_adj) \\ &\text{where,} \\ &m_adj = Date(Year(m), Month(m) - L + L_c, 1) \\\end{split}\]

  • “daily”: For any date, m, with a given index_lag performs calendar day interpolation on surrounding “monthly” values.

    \[\begin{split}&I^{daily}_v(m) = I^{monthly}_v(m) + \frac{Day(m) - 1}{n} \left ( I^{monthly}_v(m_+) - I^{monthly}_v(m) \right ) \\ &\text{where,} \\ &m_+ = \text{Any date in the month following, }m &n = \text{Calendar days in, } Month(m)\end{split}\]

Examples

The SWESTR rate, for reference value date 6th Sep 2021, was published as 2.375% and the RFR index for that date was 100.73350964. Below we calculate the value that was published for the RFR index on 7th Sep 2021 by the Riksbank.

In [5]: index_curve = Curve(
   ...:     nodes={
   ...:         dt(2021, 9, 6): 1.0,
   ...:         dt(2021, 9, 7): 1 / (1 + 2.375/36000)
   ...:     },
   ...:     index_base=100.73350964,
   ...:     convention="Act360",
   ...:     index_lag=0,
   ...: )
   ...: 

In [6]: index_curve.rate(dt(2021, 9, 6), "1d")
Out[6]: 2.3750000000015703

In [7]: index_curve.index_value(dt(2021, 9, 7), 0)
Out[7]: 100.7401552534832
plot(tenor, right=NoInput.blank, left=NoInput.blank, comparators=NoInput.blank, difference=False, labels=NoInput.blank)#

Plot given forward tenor rates from the curve. See notes.

Parameters:

  • tenor (str) – The tenor of the forward rates to plot, e.g. “1D”, “3M”.

  • right (datetime or str, optional) – The right bound of the graph. If given as str should be a tenor format defining a point measured from the initial node date of the curve. Defaults to the final node of the curve minus the tenor.

  • left (datetime or str, optional) – The left bound of the graph. If given as str should be a tenor format defining a point measured from the initial node date of the curve. Defaults to the initial node of the curve.

  • comparators (list[Curve]) – A list of curves which to include on the same plot as comparators.

  • difference (bool) – Whether to plot as comparator minus base curve or outright curve levels in plot. Default is False.

  • labels (list[str]) – A list of strings associated with the plot and comparators. Must be same length as number of plots.

Returns:

(fig, ax, line)

Return type:

Matplotlib.Figure, Matplotplib.Axes, Matplotlib.Lines2D

Notes

This function plots single-period, simple interest curve rates, which are defined as:

\[1 + r d = \frac{v_{start}}{v_{end}}\]

where d is the day count fraction determined using the convention associated with the Curve.

This function does not plot swap rates, which is impossible since the Curve object contains no information regarding the parameters of the ‘swap’ (e.g. its frequency or its convention etc.). If tenors longer than one year are sought results may start to deviate from those one might expect. See Issue 246.

plot_index(right=NoInput.blank, left=NoInput.blank, comparators=NoInput.blank, difference=False, labels=NoInput.blank, interpolation='curve')#

Plot given index values on a Curve.

Parameters:

  • right (datetime or str, optional) – The right bound of the graph. If given as str should be a tenor format defining a point measured from the initial node date of the curve. Defaults to the final node of the curve minus the tenor.

  • left (datetime or str, optional) – The left bound of the graph. If given as str should be a tenor format defining a point measured from the initial node date of the curve. Defaults to the initial node of the curve.

  • comparators (list[Curve]) – A list of curves which to include on the same plot as comparators.

  • difference (bool) – Whether to plot as comparator minus base curve or outright curve levels in plot. Default is False.

  • labels (list[str]) – A list of strings associated with the plot and comparators. Must be same length as number of plots.

  • interpolation (str in {"curve", "daily", "monthly"}) – The type of index interpolation method to use.

Returns:

(fig, ax, line)

Return type:

Matplotlib.Figure, Matplotplib.Axes, Matplotlib.Lines2D

rate(effective, termination=NoInput.blank, modifier=NoInput.inherit, float_spread=NoInput.blank, spread_compound_method=NoInput.blank)#

Calculate the rate on the Curve using DFs.

If rates are sought for dates prior to the initial node of the curve None will be returned.

Parameters:

  • effective (datetime) – The start date of the period for which to calculate the rate.

  • termination (datetime or str) – The end date of the period for which to calculate the rate.

  • modifier (str, optional) – The day rule if determining the termination from tenor. If False is determined from the Curve modifier.

  • float_spread (float, optional) – A float spread can be added to the rate in certain cases.

  • spread_compound_method (str in {"none_simple", "isda_compounding"}) – The method if adding a float spread. If “none_simple” is used this results in an exact calculation. If “isda_compounding” or “isda_flat_compounding” is used this results in an approximation.

Return type:

Dual, Dual2 or float

Notes

Calculating rates from a curve implies that the conventions attached to the specific index, e.g. USD SOFR, or GBP SONIA, are applicable and these should be set at initialisation of the Curve. Thus, the convention used to calculate the rate is taken from the Curve from which rate is called.

modifier is only used if a tenor is given as the termination.

Major indexes, such as legacy IBORs, and modern RFRs typically use a convention which is either “Act365F” or “Act360”. These conventions do not need additional parameters, such as the termination of a leg, the frequency or a leg or whether it is a stub to calculate a DCF.

Adding Floating Spreads

An optimised method for adding floating spreads to a curve rate is provided. This is quite restrictive and mainly used internally to facilitate other parts of the library.

  • When spread_compound_method is “none_simple” the spread is a simple linear addition.

  • When using “isda_compounding” or “isda_flat_compounding” the curve is assumed to be comprised of RFR rates and an approximation is used to derive to total rate.

Examples

In [8]: curve_act365f = Curve(
   ...:     nodes={
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2022, 2, 1): 0.98,
   ...:         dt(2022, 3, 1): 0.978,
   ...:     },
   ...:     convention='Act365F'
   ...: )
   ...: 

In [9]: curve_act365f.rate(dt(2022, 2, 1), dt(2022, 3, 1))
Out[9]: 2.6657902424774402

Using a different convention will result in a different rate:

In [10]: curve_act360 = Curve(
   ....:     nodes={
   ....:         dt(2022, 1, 1): 1.0,
   ....:         dt(2022, 2, 1): 0.98,
   ....:         dt(2022, 3, 1): 0.978,
   ....:     },
   ....:     convention='Act360'
   ....: )
   ....: 

In [11]: curve_act360.rate(dt(2022, 2, 1), dt(2022, 3, 1))
Out[11]: 2.6292725679229547
roll(tenor, id=NoInput.blank)#

Create a RolledCurve: translating the rate space of Self in time.

For examples see the documentation for RolledCurve.

Parameters:

  • tenor (datetime, str or int) – The measure of time by which to translate the curve through time.

  • id (str, optional) – Set the id of the returned curve.

Return type:

RolledCurve

shift(spread, id=NoInput.blank)#

Create a ShiftedCurve: moving Self vertically in rate space.

For examples see the documentation for ShiftedCurve.

Parameters:

  • spread (float, Dual, Dual2, Variable) – The number of basis points added to the existing curve.

  • id (str, optional) – Set the id of the returned curve.

Return type:

ShiftedCurve

to_json()#

Serialize this object to JSON format.

The object can be deserialized using the from_json() method.

Return type:

str

Notes

Some Curves will not be serializable, for example those that possess user defined interpolation functions.

translate(start, id=NoInput.blank)#

Create a TranslatedCurve: maintaining an identical rate space, but moving the initial node date forwards in time.

For examples see the documentation for TranslatedCurve.

Parameters:

  • start (datetime) – The new initial node date for the curve. Must be after the original initial node date.

  • id (str, optional) – Set the id of the returned curve.

Return type:

TranslatedCurve

update(nodes=NoInput.blank)#

Update a curves nodes with new, manually input values.

For arguments see Curve. Any value not given will not change the underlying Curve.

Parameters:

nodes (dict[datetime, DualTypes], optional) – New nodes to assign to the curve.

Return type:

None

Notes

Warning

Rateslib is an object-oriented library that uses complex associations. Although Python may not object to directly mutating attributes of a Curve instance, this should be avoided in rateslib. Only use official update methods to mutate the values of an existing Curve instance. This class is labelled as a mutable on update object.

update_meta(key, value)#

Update a single meta value on the Curve.

Parameters:

  • key (datetime) – The meta descriptor to update. Must be a documented attribute of _CurveMeta.

  • value (Any) – Value to update on the Curve.

Return type:

None

update_node(key, value)#

Update a single node value on the Curve.

Parameters:

  • key (datetime) – The node date to update. Must exist in nodes.

  • value (float, Dual, Dual2, Variable) – Value to update on the Curve.

Return type:

None

Notes

Warning

Rateslib is an object-oriented library that uses complex associations. Although Python may not object to directly mutating attributes of a Curve instance, this should be avoided in rateslib. Only use official update methods to mutate the values of an existing Curve instance. This class is labelled as a mutable on update object.