[1]:
from rateslib import *
Constructing Curves from (CC) Zero Rates#
A common type of curve definition in quantitative analysis is to construct a Curve from continuously compounded zero coupon rates.
There is a one-to-one equivalence relation between discount factors (DFs) and cc zero rates:
where \(d\) is the day count fraction (DCF) measured between ‘today’ and the ‘maturity’ date of the rate, using the convention assocoiated with the rates.
In rateslib a Curve is defined by DF nodes, so if one wants to construct a Curve from zero rates either these have to be manually converted to DFs or the Solver can be used to determine them via calibration.
Direct conversion#
Writing a manual conversion function is not difficult. We just need to use the above formula directly.
[2]:
def curve_from_zero_rates(nodes, convention, calendar):
start = list(nodes.keys())[0]
nodes_ = {
**{date: dual_exp(-dcf(start, date, convention=convention) * r/100.0)
for (date,r) in list(nodes.items())}
}
return Curve(nodes=nodes_, convention=convention, calendar=calendar)
[3]:
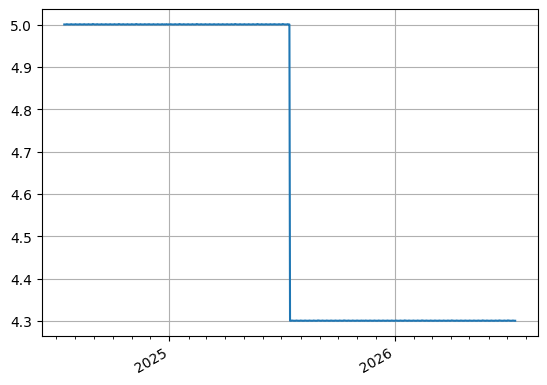
curve = curve_from_zero_rates(
{dt(2024, 7, 15): 0.0, dt(2025, 7, 15): 5.00, dt(2026, 7, 15): 4.65},
convention="act365f",
calendar="nyc",
)
curve.plot("1d")
[3]:
(<Figure size 640x480 with 1 Axes>,
<Axes: >,
[<matplotlib.lines.Line2D at 0x115c216d0>])
[4]:
curve.nodes
[4]:
{datetime.datetime(2024, 7, 15, 0, 0): 1.0,
datetime.datetime(2025, 7, 15, 0, 0): 0.951229424500714,
datetime.datetime(2026, 7, 15, 0, 0): 0.9111935002961405}
If cubic spline interpolation was required this could be included within the curve_from_zero_rates function using the t argument from a Curve.
Using a Solver#
The advantage of using a Solver is that the Curve can be calibrated directly without a manually written construction function and derivatives and risk sensitivities are automatically obtained. The easiest way to directly specify this is to use the Value class.
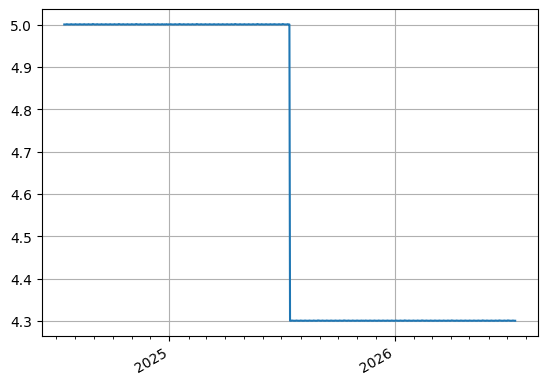
[5]:
curve = Curve(
{dt(2024, 7, 15): 1.0, dt(2025, 7, 15): 1.0, dt(2026, 7, 15): 1.0},
convention="act365f", calendar="nyc", id="ccz_curve"
)
solver = Solver(
curves=[curve],
instruments=[
Value(dt(2025, 7, 15), "act365f" ,metric="cc_zero_rate", curves=curve),
Value(dt(2026, 7, 15), "act365f" ,metric="cc_zero_rate", curves=curve),
],
s=[5.0, 4.65] # <- Same rates to observe same derived discount factors
)
SUCCESS: `func_tol` reached after 4 iterations (levenberg_marquardt), `f_val`: 7.99937338613464e-16, `time`: 0.0013s
[6]:
curve.plot("1d")
[6]:
(<Figure size 640x480 with 1 Axes>,
<Axes: >,
[<matplotlib.lines.Line2D at 0x115f1b110>])
[7]:
curve.nodes
[7]:
{datetime.datetime(2024, 7, 15, 0, 0): <Dual: 1.000000, (ccz_curve0, ccz_curve1, ccz_curve2), [1.0, 0.0, 0.0]>,
datetime.datetime(2025, 7, 15, 0, 0): <Dual: 0.951229, (ccz_curve0, ccz_curve1, ccz_curve2), [0.0, 1.0, 0.0]>,
datetime.datetime(2026, 7, 15, 0, 0): <Dual: 0.911194, (ccz_curve0, ccz_curve1, ccz_curve2), [0.0, 0.0, 1.0]>}
