User Guide#

Where to start?#

Rateslib tends to follow the typical quant architecture:

Library pricing framework

This means that financial instrument specification, curve and/or surface construction from market data including foreign exchange (FX) will permit pricing metrics and risk sensitivity. These functionalities are interlinked and potentially dependent upon each other. This guide will introduce them in a structured way and give typical examples how they are used in practice.

Let’s start with some fundamental Curve and Instrument constructors.

Trivial derivatives examples#

Rateslib has two fundamental Curve types. Most of the time you will only need to use a Curve.

A Curve is discount factor (DF) based and is constructed by providing DFs on specific node dates. Interpolation between nodes is configurable, but the below uses the “log-linear” default.

In [1]: from rateslib import *

In [2]: usd_curve = Curve(
   ...:     nodes={
   ...:         dt(2022, 1, 1): 1.0,
   ...:         dt(2022, 7, 1): 0.98,
   ...:         dt(2023, 1, 1): 0.95
   ...:     },
   ...:     calendar="nyc",
   ...:     id="sofr",
   ...: )
   ...:

Next, we will construct some basic derivative Instruments. These will use some market conventions defined by rateslib through its default argument specifications, although all arguments can be supplied manually if and when required.

Here we create a short dated SOFR RFR interest rate swap (IRS).

In [6]: irs = IRS(
   ...:     effective=dt(2022, 2, 15),
   ...:     termination="6m",
   ...:     notional=1000000000,
   ...:     fixed_rate=2.0,
   ...:     spec="usd_irs"
   ...: )
   ...:

We can combine the Curves and the Instruments to give pricing metrics such as npv(), cashflows(), and the mid-market rate(), as well as others. Without further specification these values are all expressed in the Instrument’s local USD settlement currency.

In [11]: irs.npv(curves=usd_curve)
Out[11]: 12629097.829705866

In [12]: irs.cashflows(curves=usd_curve)
Out[12]: 
               Type  Ccy    Payment       Notional Period Convention  DCF  Acc Start    Acc End   DF     Cashflow         NPV  FX Rate Base Ccy     NPV Ccy Collateral  Rate  Spread
leg1 0  FixedPeriod  USD 2022-08-17  1000000000.00   Stub     Act360 0.50 2022-02-15 2022-08-15 0.97 -10055555.56 -9776494.15     1.00      USD -9776494.15       None  2.00     NaN
leg2 0  FloatPeriod  USD 2022-08-17 -1000000000.00   Stub     Act360 0.50 2022-02-15 2022-08-15 0.97  23045139.84 22405591.98     1.00      USD 22405591.98       None  4.58    0.00

Securities and bonds#

Rateslib is steadily building a collection of market conventions for a host of global bonds. Again these specifications are available at default argument specifications for those that have already been populated.

A very common instrument in financial investing is a FixedRateBond. At time of writing the on-the-run 10Y US treasury was the 3.875% Aug 2033 bond. Here we construct this using the street convention and derive the price from yield-to-maturity and risk calculations.

In [23]: fxb = FixedRateBond(
   ....:     effective=dt(2023, 8, 15),
   ....:     termination=dt(2033, 8, 15),
   ....:     fixed_rate=3.875,
   ....:     spec="us_gb"  # US Government Bond
   ....: )
   ....: 

In [24]: fxb.accrued(settlement=dt(2025, 2, 14))
Out[24]: 1.9269701086956519

In [25]: fxb.price(ytm=4.0, settlement=dt(2025, 2, 14))
Out[25]: 99.10641380057267

In [26]: fxb.duration(ytm=4.0, settlement=dt(2025, 2, 14), metric="duration")
Out[26]: np.float64(7.178560455252011)

In [27]: fxb.duration(ytm=4.0, settlement=dt(2025, 2, 14), metric="modified")
Out[27]: np.float64(7.037804367894129)

In [28]: fxb.duration(ytm=4.0, settlement=dt(2025, 2, 14), metric="risk")
Out[28]: np.float64(7.11053190579773)

There are some interesting Cookbook articles on BondFuture and cheapest-to-deliver (CTD) analysis.

Quick look at FX#

Spot rates and conversion#

The above values were all calculated and displayed in USD. That is the default currency in rateslib and the local currency of those Instruments. We can convert these values into another currency using the FXRates class. This is a basic class which is parametrised by some exchange rates.

In [42]: fxr = FXRates({"eurusd": 1.05, "gbpusd": 1.25})

In [43]: fxr.rates_table()
Out[43]: 
     usd  eur  gbp
usd 1.00 0.95 0.80
eur 1.05 1.00 0.84
gbp 1.25 1.19 1.00

We now have a mechanism by which to specify values in other currencies.

In [44]: irs.npv(curves=usd_curve, fx=fxr, base="usd")
Out[44]: 12629097.829705866

In [45]: irs.npv(curves=usd_curve, fx=fxr, base="eur")
Out[45]: <Dual: 12027712.218767, (fx_eurusd), [-11454964.0]>

One observes that the value returned here is not a float but a Dual which is part of rateslib’s AD framework. This is the first example of capturing a sensitivity, which here denotes the sensitivity of the EUR NPV relative to the EURUSD FX rate. One can read more about this particular treatment of FX here and more generally about the dual AD framework here.

FX forwards#

For multi-currency derivatives we need more than basic, spot exchange rates. We need an FXForwards market. This stores the FX rates and the interest rates curves that are used for all the FX-interest rate parity derivations. With these we can calculate forward FX rates and also ad-hoc FX swap rates.

When defining the fx_curves dict mapping, the key “eurusd” should be interpreted as; the Curve for EUR cashflows, collateralised in USD, and similarly for other entries.

In [54]: eur_curve = Curve({
   ....:     dt(2022, 1, 1): 1.0,
   ....:     dt(2022, 7, 1): 0.972,
   ....:     dt(2023, 1, 1): 0.98},
   ....:     calendar="tgt",
   ....: )
   ....: 

In [55]: eurusd_curve = Curve({
   ....:     dt(2022, 1, 1): 1.0,
   ....:     dt(2022, 7, 1): 0.973,
   ....:     dt(2023, 1, 1): 0.981}
   ....: )
   ....: 

In [56]: fxf = FXForwards(
   ....:     fx_rates=FXRates({"eurusd": 1.05}, settlement=dt(2022, 1, 1)),
   ....:     fx_curves={
   ....:         "usdusd": usd_curve,
   ....:         "eureur": eur_curve,
   ....:         "eurusd": eurusd_curve,
   ....:     }
   ....: )
   ....: 

In [57]: fxf.rate("eurusd", settlement=dt(2023, 1, 1))
Out[57]: <Dual: 1.084263, (fx_eurusd), [1.0]>

In [58]: fxf.swap("eurusd", settlements=[dt(2022, 2, 1), dt(2022, 5, 2)])
Out[58]: <Dual: -37.314180, (fx_eurusd), [-35.5]>

FXForwards objects are comprehensive and more information regarding all of the FX features is available in this link.

More about instruments#

We’ve seen some single currency derivatives above. A complete guide for all of the Instruments is available in this link. That will also introduce the building blocks; Legs and Periods.

Multi-currency instruments#

Let’s take a look at the multi-currency instruments. Notice how these Instruments maintain consistent method naming conventions with those above. This makes it possible to plug any Instruments into a Solver to calibrate Curves around target mid-market rates, and generate market risks.

This is an FXSwap.

In [59]: fxs = FXSwap(
   ....:     effective=dt(2022, 2, 1),
   ....:     termination="3m",  # May-1 is a holiday, May-2 is business end date.
   ....:     pair="eurusd",
   ....:     notional=20e6,
   ....:     calendar="tgt|fed",
   ....: )
   ....: 

In [60]: fxs.rate(curves=[eurusd_curve, usd_curve], fx=fxf)
Out[60]: <Dual: -37.314180, (fx_eurusd), [-35.5]>

In [61]: fxs.cashflows_table(curves=[eurusd_curve, usd_curve], fx=fxf)
Out[61]: 
local_ccy               EUR          USD
collateral_ccy          usd          usd
payment                                 
2022-02-01     -20000000.00  20974233.02
2022-05-02      20000000.00 -20899604.66

Calibrating curves with a solver#

The guide for Constructing Curves introduces the main curve classes, Curve and LineCurve. It also touches on some of the more advanced curves CompositeCurve, ProxyCurve, and MultiCsaCurve.

Calibrating curves is a very natural thing to do in fixed income. We typically use market prices of commonly traded instruments to set values. Smiles and Surfaces are also calibrated using the same optimising algorithms.

Below we demonstrate how to calibrate the Curve that we created above in the initial trivial example using SOFR swap market data. In this case we invoke the Solver which forces mutations to the provided curves making sure they reprice the provided calibrating instruments at the gives rates s. In this case we target the 6M and 1Y IRS rates.

In [82]: solver = Solver(
   ....:     curves=[usd_curve],
   ....:     instruments=[
   ....:         IRS(dt(2022, 1, 1), "6M", spec="usd_irs", curves="sofr"),
   ....:         IRS(dt(2022, 1, 1), "1Y", spec="usd_irs", curves="sofr"),
   ....:     ],
   ....:     s=[4.35, 4.85],
   ....:     instrument_labels=["6M", "1Y"],
   ....:     id="us_rates"
   ....: )
   ....: 
SUCCESS: `func_tol` reached after 3 iterations (levenberg_marquardt), `f_val`: 3.0486414271327023e-15, `time`: 0.0012s

Solving was a success! Observe that the DFs on the Curve have been updated:

In [83]: usd_curve.nodes
Out[83]: _CurveNodes(_nodes={datetime.datetime(2022, 1, 1, 0, 0): <Dual: 1.000000, (sofr0, sofr1, sofr2), [1.0, 0.0, 0.0]>, datetime.datetime(2022, 7, 1, 0, 0): <Dual: 0.978595, (sofr0, sofr1, sofr2), [0.0, 1.0, 0.0]>, datetime.datetime(2023, 1, 1, 0, 0): <Dual: 0.953176, (sofr0, sofr1, sofr2), [0.0, 0.0, 1.0]>})

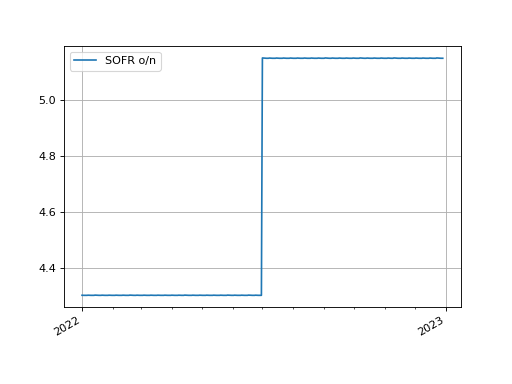
We can plot the overnight rates for the calibrated curve. This curve uses ‘log_linear’ interpolation so the overnight forward rates are constant between node dates.

In [84]: usd_curve.plot("1b", labels=["SOFR o/n"])
Out[84]: 
(<Figure size 640x480 with 1 Axes>,
 <Axes: >,
 [<matplotlib.lines.Line2D at 0x170b71a90>])

(Source code, png, hires.png, pdf)

_images/i_guide-1.png

Risk Sensitivities#

Rateslib’s can calculate delta and cross-gamma risks relative to the calibrating Instruments of a Solver. Rateslib also unifies these risks against the FX rates used to create an FXForwards market, to provide a fully consistent risk framework expressed in arbitrary currencies. See the risk framework notes.

Performance wise, because rateslib uses dual number AD upto 2nd order, combined with the appropriate analysis, it is shown to calculate a 150x150 Instrument cross-gamma grid (22,500 elements) from a calculated portfolio NPV in approximately 250ms.

Scheduling#

Necessary functionality is provided natively by rateslib. See:

Utilities#

Rateslib could not function without some utility libraries. These are often referenced in other guides as they arise and can also be linked to from those sections.

Specifically those utilities are:

Cookbook#

This is a collection of more detailed examples and explanations that don’t necessarily fall into any one category. See the Cookbook index.

Advanced Concepts#

These sections describe and exemplify some of the architectural choices in rateslib.

Pricing Mechanisms#

Since rateslib is an object oriented library with object associations we give detailed instructions of the way in which the associations can be constructed in mechanisms.

The key takeway is that when you initialise and create an Instrument you can do one of three things:

  1. Not provide any Curves (or Vol surface) for pricing upfront (curves=NoInput(0)).

  2. Create an explicit association to pre-existing Python objects, e.g. curves=my_curve.

  3. Define some reference to a Curves mapping with strings using curves="my_curve_id".

If you do 1) then you must provide Curves at price time: instrument.npv(curves=my_curve).

If you do 2) then you do not need to provide anything further at price time: instrument.npv(). But you still can provide Curves directly, like for 1), as an override.

If you do 3) then you can provide a Solver which contains the Curves and will resolve the string mapping: instrument.npv(solver=my_solver). But you can also provide Curves directly, like for 1), as an override.

Best practice in rateslib is to use 3). This is the safest and most flexible approach and designed to work best with risk sensitivity calculations also.

Mutability#

A proper outline of the mutability of objects is given in mutability.

In summary, best practice is to create new instances and avoid directly overwriting or adding to class attributes. Don’t mutate a created object unless using an official method to do so, e.g. FXRates.update or Curve.update