Building Custom Curves with _BaseCurve (e.g. Nelson-Siegel)#
The rateslib curves objects are structured in such a way that it is strightforward to create new, custom curve objects useable throughout the library, provided they implement the necessary abstract base objects. The key, heritable object that will be described on this page is _BaseCurve.
A _BaseCurve requires some default user implementation. After the completion of these elements the subclass will operate within rateslib as per any of its natural Curve constructs. This page is structured as follows;
Describe the Curve object that we wish to implement.
Setup the skeletal structure of the subclass so that it initialises without ABC related exceptions.
Develop the methods according to Curve specification.
Extend with additional methods to allow Solver interaction.
Describe the Curve: Nelson-Siegel#
This example will construct a parametric Nelson-Siegel Curve, whose continuously compounded zero rate, \(r\), at time, \(T\), is given by the following equation of four parameters, \([\beta_0, \beta_1, \beta_2, \lambda]\):
This leads to the discount factors on that curve equaling:
_BaseCurve ABCs#
First we setup the skeletal structure of our custom curve. We will inherit from _BaseCurve and setup the necessary abstract base class (ABC) properties.
Some items we know in advance regarding our custom curve:
it will return discount factors, defining its _CurveType,
it has
4parameters,we must define a
startdate (which makes its initial node) andendin its _CurveNodeswe will just inherit
metaproperty andidproperty intialisation from the _BaseCurve
[1]:
from rateslib import *
import numpy as np
from rateslib.curves import _BaseCurve, _CurveType, _CurveNodes
class NelsonSiegelCurve(_BaseCurve):
# ABC properties
_base_type = _CurveType.dfs
_id = None
_meta = None
_nodes = None
_ad = None
_interpolator = None
_n = 4
def __init__(self, start, end, beta0, beta1, beta2, lambd):
self._id = super()._id
self._meta = super()._meta
self._ad = 0
self._nodes = _CurveNodes({start: 0.0, end: 0.0})
self._params = (beta0, beta1, beta2, lambd)
# ABC required methods
def _set_ad_order(self, order):
raise NotImplementedError()
def __getitem__(self, date):
raise NotImplementedError()
This curve can now be initialised without raising any errors relating to Abstract Base Classes. However, it doesn’t do much without implementing the __getitem__ method.
[2]:
curve = NelsonSiegelCurve(dt(2000, 1, 1), dt(2010, 1, 1), 0.025, 0.0, 0.0, 0.5)
The __getitem__ method#
This method will return discount factors. If the requested date is prior to the curve: return zero as usual. If the date is the same as the initial node date: return one, else use continuously compounded rates to derive a discount factor.
This implementation, for simplcity, does not make use of the cache. However, inspection of the default _BaseCurve.__getitem__ implementation shows how to implement retrieval of values from the cache using self._cache and how to populate the cache using self._cached_value(..).
[3]:
class NelsonSiegelCurve(_BaseCurve):
_base_type = _CurveType.dfs
_id = None
_meta = None
_nodes = None
_ad = None
_interpolator = None
_n = 4
def __init__(self, start, end, beta0, beta1, beta2, lambd):
self._id = super()._id
self._meta = super()._meta
self._ad = 0
self._nodes = _CurveNodes({start: 0.0, end: 0.0})
self._params = (beta0, beta1, beta2, lambd)
def _set_ad_order(self, order):
raise NotImplementedError()
def __getitem__(self, date):
if date < self.nodes.initial:
return 0.0
elif date == self.nodes.initial:
return 1.0
b0, b1, b2, l0 = self._params
T = dcf(self.nodes.initial, date, convention=self.meta.convention, calendar=self.meta.calendar)
a1 = l0 * (1 - dual_exp(-T / l0)) / T
a2 = a1 - dual_exp(-T / l0)
r = b0 + a1 * b1 + a2 * b2
return dual_exp(-T * r)
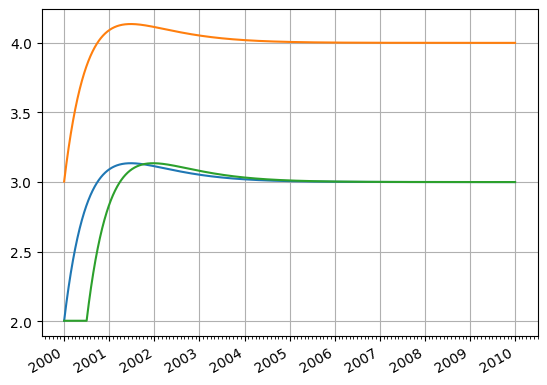
Once this method is added to the class and the discount factors are available, all of the provided methods are also available. The following snippet of code demonstrates each of the rate(), plot(), roll(), shift() and translate() methods without the user having implemented any of them:
[4]:
ns_curve = NelsonSiegelCurve(
start=dt(2000, 1, 1),
end=dt(2010, 1, 1),
beta0=0.03,
beta1=-0.01,
beta2=0.01,
lambd=0.75
)
ns_curve.plot("1b", comparators=[ns_curve.shift(100), ns_curve.roll("6m")])
[4]:
(<Figure size 640x480 with 1 Axes>,
<Axes: >,
[<matplotlib.lines.Line2D at 0x10daa74d0>,
<matplotlib.lines.Line2D at 0x10dad97f0>,
<matplotlib.lines.Line2D at 0x10dad9940>])
Mutatbility and the Solver#
In order to allow this curve to be calibrated by a Solver, we need to add some elements that allows the Solver to interact with it. We will also set the NelsonSeigelCurve to inherit _WithMutability.
Firstly, we can add the getter methods:
[5]:
_ini_solve = 0 # <- this tells the `Solver` not to 'skip' any parameters (like the initial DF of 1.0 on a `Curve`)
def _get_node_vector(self):
# this maps the curve's parameters to a consistent NumPy array consumed by the `Solver`.
return np.array(self._params)
def _get_node_vars(self):
# this get the ordered variable names of the curve's parameters for AD management.
return tuple(f"{self._id}{i}" for i in range(self._ini_solve, self._n))
The setter methods that the Solver needs are slightly more complicated. These allow the Solver to mutate the Curve directly and provide mappings.
[6]:
from rateslib.curves import _WithMutability
from rateslib.mutability import _new_state_post
from rateslib.dual import set_order_convert
from rateslib.dual.utils import _dual_float
@_new_state_post # <- this sets a new state every time the curve is mutated
def _set_node_vector(self, vector, ad):
# this maps the `Solver's` output new node values to the curve's parameters attribute with the appropriate AD number type
if ad == 0:
self._params = tuple(_dual_float(_) for _ in vector)
elif ad == 1:
self._params = tuple(
Dual(_dual_float(_), [f"{self._id}{i}"], []) for i, _ in enumerate(vector)
)
else: # ad == 2
self._params = tuple(
Dual2(_dual_float(_), [f"{self._id}{i}"], [], []) for i, _ in enumerate(vector)
)
def _set_ad_order(self, order):
# this allows the `Solver` to change the AD number type of the curve for `delta` and `gamma` calculations.
if self.ad == order:
return None
else:
self._ad = order
self._params = tuple(
set_order_convert(_, order, [f"{self._id}{i}"]) for i, _ in enumerate(self._params)
)
Adding these elements yields the final code to implement this user custom Curve class:
[7]:
class NelsonSiegelCurve(_WithMutability, _BaseCurve):
# ABC properties
_ini_solve = 0
_base_type = _CurveType.dfs
_id = None
_meta = None
_nodes = None
_ad = None
_interpolator = None
_n = 4
def __init__(self, start, end, beta0, beta1, beta2, lamb):
self._id = super()._id
self._meta = super()._meta
self._ad = 0
self._nodes = _CurveNodes({start: 0.0, end: 0.0})
self._params = (beta0, beta1, beta2, lamb)
def __getitem__(self, date):
if date < self.nodes.initial:
return 0.0
elif date == self.nodes.initial:
return 1.0
b0, b1, b2, l0 = self._params
T = dcf(self.nodes.initial, date, convention=self.meta.convention, calendar=self.meta.calendar)
a1 = l0 * (1 - dual_exp(-T / l0)) / T
a2 = a1 - dual_exp(-T / l0)
r = b0 + a1 * b1 + a2 * b2
return dual_exp(-T * r)
# Solver mutability methods
def _get_node_vector(self):
return np.array(self._params)
def _get_node_vars(self):
return tuple(f"{self._id}{i}" for i in range(self._ini_solve, self._n))
def _set_node_vector(self, vector, ad):
if ad == 0:
self._params = tuple(_dual_float(_) for _ in vector)
elif ad == 1:
self._params = tuple(
Dual(_dual_float(_), [f"{self._id}{i}"], []) for i, _ in enumerate(vector)
)
else: # ad == 2
self._params = tuple(
Dual2(_dual_float(_), [f"{self._id}{i}"], [], []) for i, _ in enumerate(vector)
)
def _set_ad_order(self, order):
if self.ad == order:
return None
else:
self._ad = order
self._params = tuple(
set_order_convert(_, order, [f"{self._id}{i}"]) for i, _ in enumerate(self._params)
)
[8]:
ns_curve = NelsonSiegelCurve(dt(2000, 1, 1), dt(2010, 1, 1), 0.03, -0.01, 0.01, 0.75)
solver = Solver(
curves=[ns_curve],
instruments=[
IRS(dt(2000, 1, 1), "2y", "A", curves=ns_curve),
IRS(dt(2000, 1, 1), "4y", "A", curves=ns_curve),
IRS(dt(2000, 1, 1), "7y", "A", curves=ns_curve),
],
s=[2.45, 2.90, 2.66],
id="NS",
instrument_labels=["2y", "4y", "7y"],
)
SUCCESS: `func_tol` reached after 8 iterations (levenberg_marquardt), `f_val`: 6.779292522573784e-13, `time`: 0.0155s
[9]:
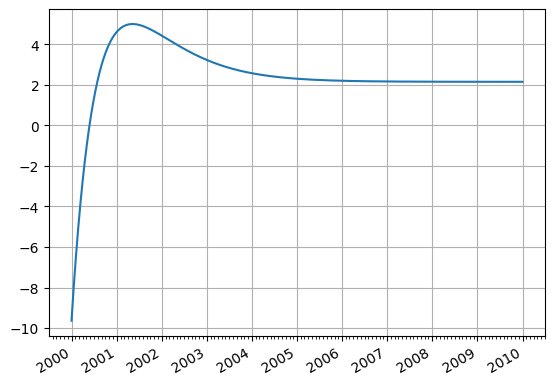
ns_curve.plot("1b")
[9]:
(<Figure size 640x480 with 1 Axes>,
<Axes: >,
[<matplotlib.lines.Line2D at 0x10da670e0>])
Risk#
Since the Solver has been invoked all typically delta and gamma methods can now also be used against this curve risk model
[10]:
portfolio = IRS(dt(2003, 7, 1), "4y", "A", notional=50e6, fixed_rate=4.5, curves=ns_curve)
portfolio.delta(solver=solver)
[10]:
| local_ccy | usd | ||
|---|---|---|---|
| display_ccy | usd | ||
| type | solver | label | |
| instruments | NS | 2y | -778.194724 |
| 4y | -22432.219524 | ||
| 7y | 42449.616358 |
[11]:
portfolio.gamma(solver=solver)
[11]:
| type | instruments | ||||||
|---|---|---|---|---|---|---|---|
| solver | NS | ||||||
| label | 2y | 4y | 7y | ||||
| local_ccy | display_ccy | type | solver | label | |||
| usd | usd | instruments | NS | 2y | 1.183954 | 1.245186 | -2.070988 |
| 4y | 1.245186 | 6.580990 | -5.017871 | ||||
| 7y | -2.070988 | -5.017871 | -17.838847 | ||||
[ ]:
